October 16^th Foundation Exam

Questions for Discrete Structures

Discrete Part I. Choose one question.

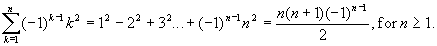
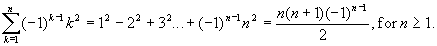
2. Let g: A ® A be a bijective function. That is, g is both one-to-one and onto. For n ³ 2, define gⁿ = g o g o … o g , where g is composed with itself n times.

Prove that for n ³ 2, (1) gⁿ is a bijective function from A to A; and (2) (gⁿ)^–1 = (g^–1)ⁿ.

Discrete Part II. Choose one question.

3. Let A = {a, b} denote a set of two symbols. Let S be a set of strings over A, satisfying the following property:

If u Î S and |u| > 0, then there exists a string v Î S such that u = avb.

Prove by induction that S Ì {aⁿbⁿ | n ³ 0}.

4. Let A = {a, b} denote a set of two symbols. Define the following two sets of strings over A:

Prove that C Ç D = {aⁿbⁿ | n ³ 0}.

Solutions to the Discrete Structures questions.