Solution Key to the Foundation Exam (Discrete Structures) on December 1998

Part I. (Choose exactly one question to answer.)

  1. Suppose x is a real number and x ¹ 1. Prove by induction that for integer n ³ 0, the following summation identity holds:

    2. Proof: We use induction on n ³ 0.

    (Basis Step) Let n = 0. In this case, since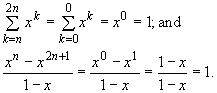

    so the summation formula is proved for the basis case.

    (Induction Hypothesis) Suppose the summation formula is true for n = m, for some m ³ 0; that is, suppose

    (Induction Step) Consider n = m + 1. We need to prove the summation formula is true in this case, that is, prove

    Note that

    LHS of (2) = xm+1 + xm+2 + … + x2m+1 + x2m+2 , by the definition of the summation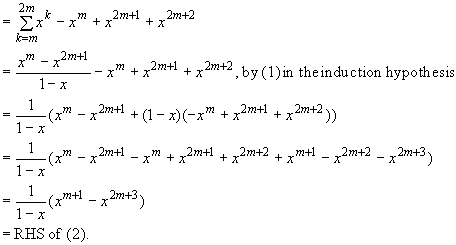

    Thus, the induction step is proved. By mathematical induction, the summation formula is true for all n ³ 0.

  2. Define a function g(n) for integer n ³ 0 by the following recurrence:

    3. g(0) = 3; g(1) = 4; and

    g(n) = 4g(n - 1) - 4g(n - 2), for n ³ 2.

    Prove that g(n) = (3 - n)2n for n ³ 0.

    Proof: We prove the formula for g(n) by using strong induction on n ³ 0.

    (Basis Step) Consider n = 0. By the formula,

    g(0) = (3 - 0)20 = 3, which is equal to the initial value of g(0).

    Similarly, when n = 1, by the formula,

    g(1) = (3 - 1)21 = 2 · 2 = 4, which is equal to the initial value of g(1).

    Thus, the formula for g(n) is true for n = 0 and n = 1.

    (Induction Hypothesis) Suppose the formula

    g(n) = (3 - n)2n is true for all n in the range 0 £ n £ k, for some k ³ 1 ------- (1).

    (Induction Step) Consider n = k + 1. We need to prove the formula is true for this case, that is, prove

    g(k + 1) = (3 - (k + 1))2k+1 ------ (2).

    Note that since k + 1 ³ 2 because k ³ 1 as stated in (1), thus, applying the recurrence of g(n),

    g(k + 1) = 4g(k + 1 - 1) - 4g(k + 1 - 2)

    = 4g(k) - 4g(k - 1)

    = 4 (3 - k)2k - 4 (3 - (k - 1))2k- 1 by the induction hypothesis (1) applied to g(k) and g(k - 1)

    = 2k- 1(4 (3 - k)2 - 4(3 - k + 1))

    = 2k- 1(24 - 8k - 12 + 4k - 4)

    = 2k- 1(8 - 4k) = 2k+1(2 - k)

    = RHS of (2).

    Thus, the induction step is proved. By mathematical induction, the formula

    g(n) = (3 - n)2n is true for n ³ 0.

    Part II. (Choose exactly one question to answer.)

    We first review and define some notations for this part. Let A = {a, b} denote an alphabet, that is a set of symbols. Recall the definition of Kleene Star:

    A* = {l } È A È A2 È … ,

    where the symbol l denote the empty string. Similarly, for any set of strings X Ì A*, define

    X* = {l } È X È X2 È …

    Now choose exactly one question from the following to answer:

  3. Consider a set of strings defined over A:

    4. L = {w | w Î A*, w either contains no occurrences of symbol b, or if w contains symbol b, then each occurrence of symbol b in w is followed immediately by at least one occurrence of symbol a}.

    Prove that L Ì {a}*({ba}{a}*)*.

    (Note that using the regular expression notation, the problem is to prove L Ì a*(baa*)*.)

    Proof: Let w Î L be an arbitrary string in L. Define the notation Nb(w) to be the number of occurrences of symbol b in string w. We now prove that w Î a*(baa*)* by using induction on Nb(w).

    (Basis Step) When Nb(w) = 0, that is, when w contains no occurrences of symbol b. In that case,

    w Î a* = a*l Ì a*(baa*)* because l Î (baa*)*.

    (Induction Hypothesis) Suppose w Î L implies w Î a*(baa*)* if Nb(w) = k, for some k ³ 0.

    (Induction Step) Consider w Î L and Nb(w) = k + 1. We need to prove w Î a*(baa*)* in this case. Since k + 1 ³ 1, the string w contains symbol b at least once. Write

    w = ubt, where the string u is a substring of w containing from the first symbol of w through the symbol immediately before the last occurrence of symbol b in w.

    Since each occurrence of symbol b in w is followed by at least one symbol a; thus,

    t Î aa*, which implies w = ubt Î ubaa*.

    Note that Nb(u) = k; also, each symbol b in string u must be followed by at least one occurrence of symbol a, because u is a substring of w. Thus, string u Î L, and the induction hypothesis applies to string u. Therefore,

    u Î a*(baa*)*, and

    w Î ubaa* Ì a*(baa*)*baa* Ì a*(baa*)*, because of the identity E*E Ì E* for any language E

    Thus, the induction step is proved. By mathematical induction, we proved that w Î L implies w Î a*(baa*)* for any string w. Therefore, L Ì a*(baa*)*.

  4. Define a function f: A* ® A* by the following recurrence rules (where A = {a, b}):
    1. f(l ) = l (where l denotes the empty string);

      2. f(a) = b; and f(b) = a;

    2. if w Î A* and |w| ³ 2, then write w = ud, where u Î A* and d Î A, define

f(w) = f(d) f(u).

Prove that f(abn) Î a*b for all n ³ 0.

Proof: We use induction on n ³ 0 to prove f(abn) Î a*b.

(Basis Step) Consider n = 0. That is, consider the string w = ab0 = al = a. In this case,

f(w) = f(a) = b by Rule (i).

Since b = l b Î a*b, because l Î a*, so we proved f(ab0) Î a*b.

(Induction Hypothesis) Suppose f(w) Î a*b, when w = abk for some k ³ 0.

(Induction Step) Consider the string w = abk+1. We need to prove f(w) Î a*b.

Note that w = abk+1= (abk)b; thus,

f(w) = f((abk)b) = f(b) f(abk) by Rule (ii)

= a f(abk) because f(b) = a by Rule (i)

Î a(a*b) by the induction hypothesis applied to f(abk)

Ì a*b because aa* Ì a*.

Thus, the induction step is proved. By mathematical induction, we proved that

f(abn) Î a*b for all n ³ 0.