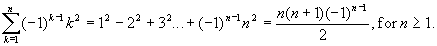
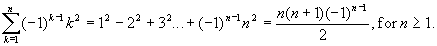
Proof: We prove this identity by using induction on n ³ 1.
(Basis Step)
Consider n = 1. The summation on the LHS is:
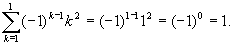
The formula on the RHS is:
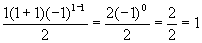
Thus, LHS = RHS, so the Basis Step is proved.
(Induction Hypothesis)
Consider n = p. Assume the identity is true for n = p, for some p ³ 1; that is, assume
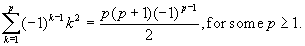
(Induction Step)
Consider n = p + 1. We need to prove the identity is true for n = p + 1; that is, we need to prove
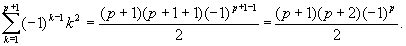
Note that
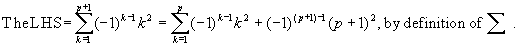
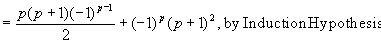
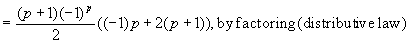
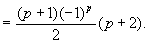
So the LHS = RHS of the Induction Step.
Therefore, the identity of the problem is true for all n ³ 1.
2. Let g: A ® A be a bijective function. That is, g is both one-to-one and onto. For n ³ 2, define gn = g o g o … o g , where g is composed with itself n times. Prove that for n ³ 2, (1) gn is a bijective function from A to A; and (2) (gn)–1 = (g–1)n.
Proof: We prove both (1) and (2) using induction on n ³ 2.
(Basis Step)
Consider n = 2. Since g: A ® A is a bijection, g2 = g o g is a bijection, by the theorem that says the compostion of two bijections is a bijection.
Also, (g2)–1 = (g o g)–1, by the definition of g2
= (g–1) o (g–1), by the theorem that says (h o f) –1= f–1 o h–1, when both f and h are bijections.
= (g–1)2, by the definition of (g–1)2.
Thus, the Basis Step is proved.
(Induction Hypothesis)
Consider n = k. Assume gk is a bijection, and (gk)–1 = (g–1)k, for some k ³ 2.
(Induction Step)
Consider n = k + 1. We need to prove (1) gk +1 is a bijection; and (2) (gk +1)–1 = (g–1)k +1.
Note that gk +1 = gk o g, by the definition of gk +1, so gk +1 is a bijection because gk is a bijection by the Induction Hypothesis, and its composition with g is also a bijection.
Further,
(gk +1)–1 = (gk o g)–1, by the definition of gk +1
= (g–1) o (gk)–1, by the theorem (h o f) –1= f–1 o h–1
= (g–1) o (g–1)k, by the Induction Hypothesis
= (g–1)k +1, by the definition of (g–1)k +1.
Thus, the Induction Step is proved.
Therefore, we have proved that (1) gn is a bijective function from A to A; and (2) (gn)–1 = (g–1)n, for all n ³ 2.
3. Let A = {a, b} denote a set of two symbols. Let S be a set of strings over A, satisfying the following property:
If u Î S and |u| > 0, then there exists a string v Î S such that u = avb.
Prove by induction that S Ì {anbn | n ³ 0}.
Proof: In order to prove S Ì {anbn | n ³ 0}, we need to prove that: if w Î S, then w Î {anbn | n ³ 0}.
We prove this statement by using induction on |w|, the length of string w.
(Basis Step)
Consider |w| = 0. In this case, w = l , the null string (you may use the symbol e.)
Since l = a0 b0, so w = l = a0 b0 Î {anbn | n ³ 0}. The Basis Step is proved.
(Induction Hypothesis)
Assume if w Î S, then w Î {anbn | n ³ 0} for all strings w with length |w| £ k, for some k ³ 0.
(Induction Step)
Consider the case if w Î S, and |w| = k + 1.
Note that |w| > 0, so there exists a string v Î S such that w = avb, by the property of S specified in the assumption. Since |v| = |w| - 2 = k + 1 - 2 = k - 1 £ k, so v Î {anbn | n ³ 0} by the Induction Hypothesis. That is,
v = ambm, for some m ³ 0.
Thus,
w = avb = a(ambm)b = am +1bm +1 Î {anbn | n ³ 0}.
So the Induction Step is proved.
Therefore, we have proved that
if w Î S, then w Î {anbn | n ³ 0} for strings w of any length |w| ³ 0.
That is, we have proved S Ì {anbn | n ³ 0}.
4. Let A = {a, b} denote a set of two symbols. Define the following two sets of strings over A:
C = {a}*{b}* , and
D = {w | w Î A*, and the number of occurrences of symbol a in w = the number of occurrences of symbol b in w}.
Prove that C Ç D = {anbn | n ³ 0}.
Proof: To prove C Ç D = {anbn | n ³ 0}, we prove
To prove (1), let string w Î C Ç D. Thus, w Î C and w Î D. Since {a}* = {an | n ³ 0} and {b}* = {bn | n ³ 0}, w Î C = {a}*{b}* implies w = ambp, for some m, p ³ 0. Also, since w Î D, m = p because the number of occurrences of symbol a in w must be equal to the number of occurrences of symbol b in w. Therefore, w = ambm Î {anbn | n ³ 0}, so (1) is proved.
To prove (2), let string w Î {anbn | n ³ 0}. Thus, w = ambm, for some m ³ 0. Therefore, w Î C ={a}*{b}*, because am Î {a}* and bm Î {b}*. Also, w Î D because the number of occurrences of symbol a in w = m = the number of occurrences of symbol b in w. Thus, w Î C Ç D, so (2) is proved.