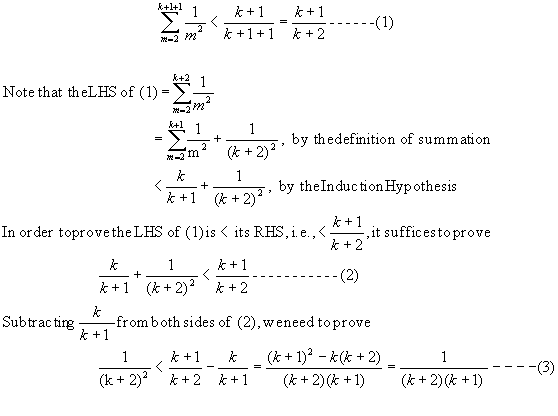Part I. Choose exactly one question (Question 1 or Question 2) in this part to answer.
- Define a function g: N ®
N by the following recurrence, where N denotes the set of natural numbers:
g(0) = 1; g(1) = 3; and
g(n) = g(n -
1) + 2 g(n -
2) -
2n + 5, for all n ³
2.
Prove by induction that g(n) = 2n + n for all n ³
0.
Solution:
Prove by induction on n ³
0 that
g(n) = 2n + n.
(Basic Step) Consider the cases of n = 0 and n = 1:
In the case that n = 0: Using the formula, g(0) = 20 + 0 = 1 + 0 = 1, which is equal to the
initial value defined for g(0).
In the case that n = 1: Using the formula, g(1) = 21 + 1 = 2 + 1 = 3, which is equal to the
initial value defined for g(1).
Thus, the formula for g(n) is correct for n = 0 and n = 1.
(Induction Hypothesis) Suppose the formula g(n) = 2n + n is correct for all n in the range
0 £
n £
k, for some k ³
1.
(Induction Step) Consider n = k + 1. We need to prove g(k+1) = 2k+1 + (k+1) -------(1)
Note that g(k+1) = g(k+1-
1) + 2g(k+1-
2) – 2(k+1) + 5, by applying the recurrence to
g(k+1), since k + 1 ³
1 + 1 = 2.
= g(k) + 2g(k-
1) – 2k – 2 + 5
= (2k + k) + 2(2k-
1+ k-
1) – 2k + 3, by applying the induction hypothesis to
g(k) and g(k-
1)
= 2k + k + 2k + 2k – 2 – 2k + 3
= 2(2k) + k + 1
= 2k+1 + k + 1
= RHS of (1)
Thus, the induction step is proved. By induction, we proved g(n) = 2n + n for all n ³
0.
- Prove by induction that
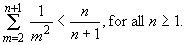
Solution: We use induction on n ³
1.
(Basic Step) Consider n = 1.
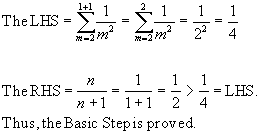
 (Induction Hypothesis) Consider n = k.
(Induction Hypothesis) Consider n = k.
(Induction Step) Consider n = k+1. We need to prove
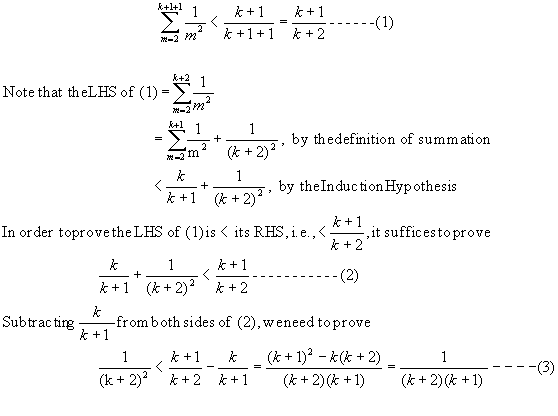
Note that (3) is true because (k + 2)2 > (k + 2)(k +1).
Thus, the induction step is proved. By induction, we proved the problem.
Part II. Choose exactly one question (Question 3 or Question 4) in this part to answer.
- Let A and B denote two non-empty sets, and let R and S denote two binary relations where R Ì
A ´
B and S Ì
A ´
B. Answer the following two parts for this question:
- Suppose both R and R Ç
S define a function from A to B. Prove that R Ì
S.
- (This part is independent of Part (a).) Suppose both R and R È
S define a function from A to B. Prove that S Ì
R.
Solution:
(a) In order to prove R Ì
S, let (x, y) Î
R ----(1), we need to prove (x, y) Î
S ----(2).
Since R Ç
S defines a function from A to B, there exists a pair (x, z) Î
R Ç
S ----(3) for some z Î
B; that is, for xÎ
A, the function R Ç
S maps x to z Î
B. From (3), (x, z) Î
R Ç
S Ì
R.
Thus, both (x, y) Î
R, from (1), and (x, z) Î
R. However, R defines a function from A to B by assumption; thus, x must be mapped under R to a unique element in B, i.e. y = z. Therefore,
(x, y) = (x, z) Î
R Ç
S, by (3)
Ì
S, by the definition of Ç
.
Thus, (2) is proved.
- In order to prove S Ì
R, let (x, y) Î
S ---(4), we need to prove (x, y) Î
R ----(5).
Since R defines a function from A to B, R maps x to some element z Î
B, i.e., (x, z) Î
R --(6)
Therefore, (x, y) Î
S Ì
R È
S and (x, z) Î
R Ì
R È
S. Since R È
S defines a function from A to B, it maps x to a unique element in B, i.e., y = z. Therefore, (x, y) = (x, z) Î
R, by (6).
Thus, (5) is proved.
- Let A = {a, b} denote an alphabet of two distinct symbols. Define a function g: A* ®
A* by the following recursive rules:
- g
(l
) = l
, where l
denotes the empty string.
- g
(a) = b.
- g
(bu) = bg(u) for any u Î
A*.
- g
(aau) = g(au) for any u Î
A*.
- g
(abu) = bg(bu) for any u Î
A*.
Prove by induction that g(anb) = b2, for all n ³
1.
Solution:
We use induction on n ³
1 to prove g(anb) = b2.
(Basic Step) When n = 1. In this case,
g(anb) = g(ab)
= g(abl
), because ab = abl
= bg(bl
), Rule (5)
= bbg(l
), Rule (3)
= b2l
, Rule (1)
= b2, because b2l
= b2.
Thus, the Basis step is proved.
(Induction Hypothesis) Consider n = k.
Assume g(akb) = b2 for some k ³
1.
(Induction Step) Consider n = k + 1. We need to prove g(ak+1b) = b2 ----(1)
Note that g(ak+1b) = g(aaak-
1b), since k ³
1 so k + 1 ³
2
= g(aak-
1b), Rule (4) with u= ak-
1b
= g(akb)
= b2, by the I.H.
Thus, the induction step is proved. By induction, we proved g(anb) = b2 for all n ³
1.
![]()
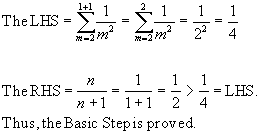
![]() (Induction Hypothesis) Consider n = k.
(Induction Hypothesis) Consider n = k.